Langsung ke konten utama

Susunan Kapasitor



Begaimana mengukur pada kapasitor? Dua atau lebih kapasitor dapat disusun secara seri (berderet),pararel (sejajar), atau gabungan antara seri dan pararel.

a.  Susunan Seri Kapasitor
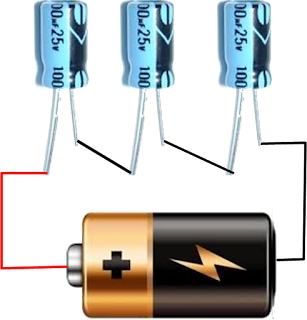
Tiga  kapasitor yang disusun seperti gabar berikut dinama-kan susunan seri.

Kita dapat mengganti tiga buah kapasitor itu dengan sebuah kapasitor pengganti yang memiliki kapasitas Cs.Pada susunan seri kapasitor berlaku:
  • Muatan pada tiap-tiap kapasitor adalah sama yaitu sama denga muatan pada kapasitor pengganti. Q = Q1 = Q2 = Q3
  • Beda potensial pada ujung-ujung kapasitor pengganti sama dengan jumlah beda potensial ujung-ujung tiap-tiap kapasitor, V = V1 + V2  +  V3
 
         









Jadi, kapasitas pengganti susunan seri beberapa buah kapasitor selalu lebih kecil daripada kapasitas tiap-tiap kapasitor. Ini berarti, untuk mendapat kapasitas terkecil maka kapasitas kapasitor disusun seri.

contoh soal
Tiga buah kapasitor yang masing-masing kapasitasnya 3  PF, 12  PF,dan 4  PF dihubungkan secara seri kemudian dipasang pada sumbertegangan sebesar 24 Volt.
Hitunglah :
a. kapasitas kapasitor susunan seri  tersebut,
b. muatan total pada kapasitor,
c. muatan masing-masing kapasitor, dan
d. tegangan pada masing-masing kapasitor!
Penyelesaian :











Soal Latihan :
1. Empat buah kapasitor yang masing-masing kapasitasnya 4 PF,  8 PF, 16 PF, dan 4 PF disusun seri kemudian dipasang pada sumber tegangan 32 Volt. Hitunglah :
a. kapasitas kapasitor susunan seri  tersebut,
b. muatan total pada kapasitor,
c. muatan masing-masing kapasitor, dan
d. tegangan pada masing-masing kapasitor!
2. Tiga buah kapasitor yang masing-masing kapasitasnya sebesar 12  PF, 24 PF, dan 6 PF disusun seri kemudian dihubungkan dengan sumber tegangan 12 Volt. Hitunglah :
a. kapasitas kapasitor susunan seri tersebut,
b. muatan total pada kapasitor,
c. muatan masing-masing kapasitor, dan


b.  Susunan Pararel Kapasitor
Dua kapasitor yang disusun pada gambar (a) berikut ini disebut susunan pararel.


Kita dapat mengganti dua buah kapasitor itu dengan sebuah kapasitor pengganti yang memiliki kapasitas Cp. Pada susunan pararel kapasitor berlaku:
Pada susunan pararel kapasitor berlaku:
  • Beda potensial tiap-tiap kapasitor sama, dan bernilai sama dengan potensial sumber. V = V1 = V2 =V3
  •  Muatan kapasitor sama dengan jumlah muatan tiap-tiap kapasitor. Q = Q1 + Q2+ Q3 

           

Contoh Soal
Tiga buah kapasitor yang masing-masing kapasitasnya 4 PF,  6 PF,  dan 12 PF disusun paralel kemudian susunan tersebut dihubungkan dengan sumber tegangan sebesar 16 Volt. Hitunglah :
a. kapasitas kapasitor susunan paralel tersebut,
b. muatan total yang tersimpan pada kapasitor,
c. tegangan pada masing-masing kapasitor, dan
d. muatan pada masing-masing kapasitor!

Penyelesaian













Soal Latihan :
1. Dua buah kapasitor masing-masing besarnya 6 PF dan 12  PF disusun secara paralel yang kemudian dipasang pada tegangan 24 Volt. Hitunglah :
a. kapasitas kapasitor susunan paralel tersebut,
b. muatan total yang tersimpan pada kapasitor,
c. tegangan pada masing-masing kapasitor, dan
d. muatan pada masing-masing kapasitor!

2. Tiga buah kapasitor masing-masing kapasitasnya 8 PF, 12 PF, dan 24 PF disusun paralel kemudian dihubungkan dengan sumber tegangan sebesar 24 Volt. Hitunglah :
a. kapasitas kapasitor susunan paralel tersebut,
b. muatan total yang tersimpan pada kapasitor,
c. tegangan pada masing-masing kapasitor, dan
d. muatan pada masing-masing kapasitor!

3. Empat buah kapasitor tersusun seperti Gambar 4.26.
C1 = 300 μF,  C2 = 400 μF,  C3 = 500 μF dan C4 = 600 μF. Jika rangkaian dihubungkan beda potensial 80volt maka tentukan :
a. Kapasitas pengganti,
b.  muatan yang tersimpan di masing-masing kapasitor,
c. beda potensial Vab dan Vbc?


LINK FISIKA
|| HOME || BENDA BERMUATAN LISTRIK || HUKUM COULOMB || MEDAN MAGNET || FLUKS LISTRIK || POTENSIAL LISTRIK  || ENERGI POTENSIAL LISTRIK || KAPASITOR |KAPASITAS KAPASITOR || ENERGI KAPASITOR || SUSUNAN KAPASITOR ||

Label:

Postingan populer dari blog ini

Gaya Magnetik di Antara Dua Kawat Sejajar Berarus

Di sekitar kawat berarus timbul induksi magnet. Apa yang akan terjadi jika kawat berarus lain didekatkan  kawat pertama? Keadaan ini berarti ada dua kawat   sejajar. Kawat kedua berada dalam induksi magnet kawat pertama, sehingga akan terjadi gaya Lorentz. Begitu juga pada kawat kedua akan menimbulkan gaya Lorentz pada kawat pertama. Gaya itu sama besar dan memenuhi persamaan berikut.       CONTOH 5.5 Diketahui dua buah kawat sejajar dialiri arus I 1 = 10 A dan I 2 = 20 A dengan arah berlawanan dan berjarak 10 cm. Tentukan gaya Lorentz yang dirasakan oleh kawat I 2 sepanjang 20 cm karena pengaruh I 1 ! Penyelesaian I1 =  10 A I2 =  20 A a  =  10 cm l = 20 cm = 0,2 m Gaya Lorentz I 2 oleh I 1 adalah : F = 4.10 -4 . 0,2 = 0,8 .10 -4 N LATIHAN 5.5 Dua kawat sejajar lurus panjang berjarak 20 cm satu sama lain. Kedua kawat dialiri arus masing-masing I 1 = 10A dan I 2 = 20 A dengan arah berlawanan. Tentukan arah dan besar gaya Lorentz yang di
Baca selengkapnya

Transformasi Lorentz (relativitas Kecepatan)

Pada transformasi Galileo telah dikemukakan bahwa selang waktu pengamatan terhadap suatu peristiwa yang diamati oleh pengamat yang diam dengan pengamat yang relatif bergerak terhadap peristiwa adalah sama ( t = t’ ) . Hal inilah yang menurut Einstein tidak benar, selang waktu pengamatan antara pengamat yang diam dan pengamat yang bergerak relatif adalah tidak sama ( t ≠ t’ ) . Transformasi Lorentz pertama kali dikemukaan oleh Hendrik A. Lorentz, seorang fisikawan dari Belanda   pada tahun 1895. Karena waktu pengamatan oleh pengamat yang diam pada kerangka acuan S dan pengamat yang bergerak pada kerangka acuan S’ hubungan transformasi pada Galileo haruslah mengandung suatu tetapan pengali   yang disebut tetapan transformasi.   Sehingga persamaan yang menyatakan hubungan antara koordinat pada kerangka acuan S dan S’ dituliskan sebagai berikut : Transformasi Lorentz          x’ =   ϒ (x – v.t), y’ = y, z’ = z    dan    t’ ≠ t                   .... (9.6) Kebali
Baca selengkapnya

Listrik Dinamis

LINK FISIKA || HOME || ARUS LISTRIK || BEDA POTENSIAL || HUKUM OHM || HAMBATAN LISTRIK || HUKUM KIRCHOFF || RANGKAIAN HAMBATAN || DAYA LISTRIK || PENGHEMATAN ENERGI ||  
Baca selengkapnya